Understanding the parts of a right-angled triangle—hypotenuse, base, and perpendicular—is key to mastering Class 10 Trigonometry. These three sides form the foundation for calculating ratios like sine, cosine, and tangent, and are critical in real-life applications such as construction, architecture, and physics.

 What is a Right-Angled Triangle?

A right-angled triangle is a triangle where one angle is exactly 90°. The side opposite the 90° angle is always the hypotenuse, and the other two sides are called base and perpendicular, depending on the reference angle.

Properties:

• One angle = 90°

• Hypotenuse is the longest side

• The other two sides are adjacent and opposite to the chosen angle

 Step-by-Step: How to Identify the Hypotenuse

• Step 1: Locate the 90° angle (marked by a square).

• Step 2: The side directly opposite the 90° angle is the hypotenuse.

• Step 3: It is always the longest side in a right triangle.

Example:
In triangle ABC, ∠B = 90°
Then, AC is the hypotenuse.

 How to Identify Base and Perpendicular

Once you know the hypotenuse, the remaining two sides depend on the reference angle (other than 90°).

• Base (Adjacent Side): The side that touches the reference angle (excluding the hypotenuse)

• Perpendicular (Opposite Side): The side opposite to the reference angle

 Example:

In triangle ABC, ∠B = 90°, and ∠A is the reference angle.

• AC = Hypotenuse (opposite 90°)

• AB = Perpendicular (opposite ∠A)

• BC = Base (touches ∠A and 90°)

Using a Diagram

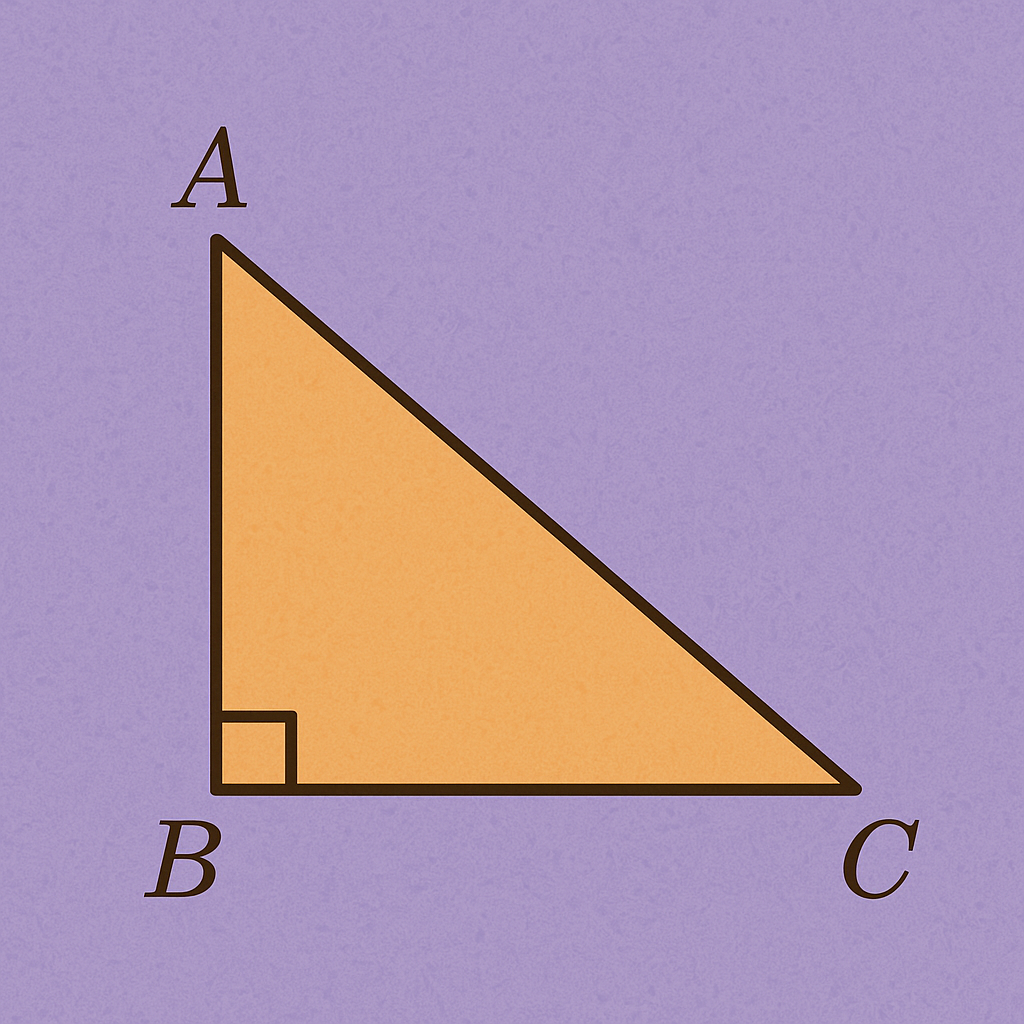
If ∠B = 90° and ∠A is the reference:

• AC = Hypotenuse

• AB = Perpendicular

• BC = Base

 Tips to Remember

• Hypotenuse is always fixed (opposite 90°)

• Base and Perpendicular depend on which angle you’re using as reference

• Label the triangle with angles first, then sides

•  Trigonometric ratios:

  • Sine(θ) = Perpendicular / Hypotenuse

  • Cosine(θ) = Base / Hypotenuse

  • Tangent(θ) = Perpendicular / Base

  • Cosec(θ) = Hypotenuse / Perpendicular

  • Sec(θ) = Hypotenuse / Base

  • Cot(θ) = Base / Perpendicular

Real-Life Example

Imagine a ladder leaning against a wall:

• The wall is the perpendicular

• The ground is the base

• The ladder is the hypotenuse

This is how right triangles work in real life too!

FAQs

Q1. What is the hypotenuse in any triangle?
A1. Only right triangles have a hypotenuse—it is the side opposite the right angle and always the longest.

Q2. Can the base and perpendicular be interchanged?
A2. Yes, depending on the angle taken as reference, the base and perpendicular change roles.

Q3. How do I know which side is perpendicular?
A3. The side that does not touch the angle you’re referencing (other than the right angle) is the perpendicular.

Q4. Do trigonometric ratios apply only to right-angled triangles?
A4. Yes, the basic ratios like sin, cos, and tan are defined using right-angled triangles.

 Conclusion:

Identifying the hypotenuse, base, and perpendicular in a right triangle is a simple but important skill for Class 10 Trigonometry. Always start by spotting the 90° angle, label the hypotenuse, and use your reference angle to find the base and perpendicular. This clarity will make all trigonometric formulas much easier to apply.

Check out another Article :

Master Maths Online with Aman Sir — Free Class 10 Demo Available!