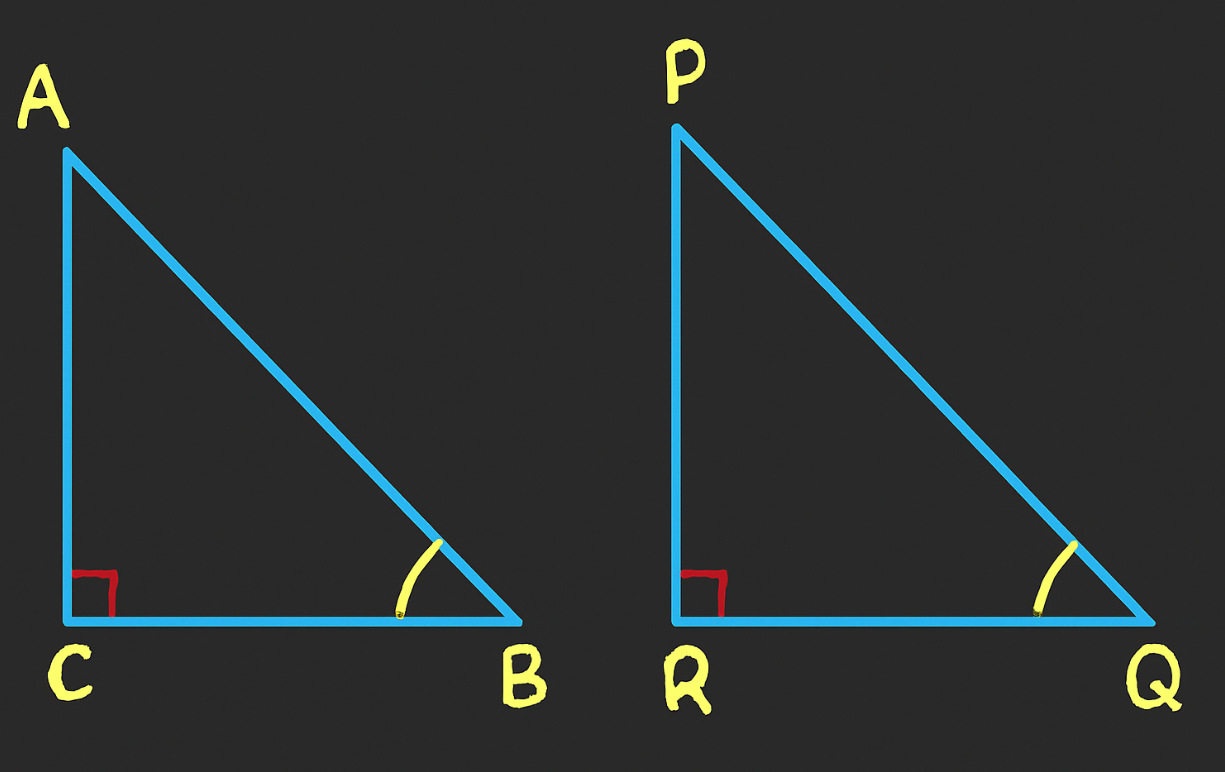VIDEO
To Prove:
∠ B = ∠ Q \angle B = \angle Q Given:
∠B and ∠Q are acute angles
sin B = sin Q
Proof:
Let us consider two right triangles:
ΔABC , right-angled at CΔPQR , right-angled at R
Step 1: Write sine values in each triangle
In ΔABC:
sin B = A C A B ⋯ ( 1 ) \sin B = \frac{AC}{AB} \quad \cdots (1)
In ΔPQR:
sin Q = P R P Q ⋯ ( 2 ) \sin Q = \frac{PR}{PQ} \quad \cdots (2)
Since given sin B = sin Q ,
A C A B = P R P Q \frac{AC}{AB} = \frac{PR}{PQ} Cross multiply:
A C P R = A B P Q = k ⋯ ( 3 ) \frac{AC}{PR} = \frac{AB}{PQ} = k \quad \cdots (3)
Step 2: Apply Pythagoras theorem
In ΔABC:
A B 2 = A C 2 + B C 2 AB^2 = AC^2 + BC^2 B C 2 = A B 2 − A C 2 ⋯ ( 4 ) BC^2 = AB^2 – AC^2 \quad \cdots (4) In ΔPQR:
P Q 2 = P R 2 + Q R 2 PQ^2 = PR^2 + QR^2 Q R 2 = P Q 2 − P R 2 ⋯ ( 5 ) QR^2 = PQ^2 – PR^2 \quad \cdots (5)
Step 3: Substitute proportionality
From (3):
A C = k ⋅ P R , A B = k ⋅ P Q AC = k \cdot PR, \quad AB = k \cdot PQ Substitute in (4):
B C 2 = ( k P Q ) 2 − ( k P R ) 2 BC^2 = (kPQ)^2 – (kPR)^2 B C 2 = k 2 ( P Q 2 − P R 2 ) BC^2 = k^2(PQ^2 – PR^2) B C Q R = k ⋯ ( 6 ) \frac{BC}{QR} = k \quad \cdots (6)
Step 4: Collect all equal ratios
From (3) and (6):
A C P R = A B P Q = B C Q R = k \frac{AC}{PR} = \frac{AB}{PQ} = \frac{BC}{QR} = k
Step 5: Conclude similarity
Since the three sides of the two triangles are proportional,
△ A B C ∼ △ P Q R \triangle ABC \sim \triangle PQR Hence,
∠ B = ∠ Q \angle B = \angle Q
If you’re looking to build a strong foundation in Maths from Class 8 to Class 12,
Tagged acute angle proof , aman sir , CBSE Maths , chapter 8 , class 10 maths , example 2 , maths teacher India , Maths Vidya Institute , NcertMaths , sin B equals sin Q , trigonometry proof